Analysing Taasen - part 1

originally posted at https://comicalmomentum.tumblr.com/po...

In this post I’m going to try and break down the game Taasen, a Chess-like board game designed by Jennifer Diane Reitz (of COGIATI infamy) for her webcomic Unicorn Jelly, which I’m reading over on @comicalmomentum.

How Taasen is played:

To briefly summarise the game: there are two players, and three coloured sets of three pieces. On their turn, the players can move either their own colour (red or green) or the ‘neutral’ blue pieces to an edge-adjacent tri. Pieces start sharing the corner tris, but can’t move to share a tri after that. The central blue tri is special: if a piece moves on to it, it must immediately make a second move off of it to a free square and not the one it started from.

After a piece moves, it triggers ‘pushing’ according to a rock-paper-scissors system: if there is an adjacent piece of the appropriate type and a different colour, the defending player is forced to move it to a free tri; if there is no free tri then it is destroyed. Edit: Pieces moved by being pushed do not cause further pushing. If a move could result in two different pieces being pushed, the attacking player picks one to push.

The three types of piece are called Thaum, Sciane and Paupil; Thaum pushes Sciane pushes Paupil pushes Thaum.

Players can’t move a blue piece moved by a player in a previous turn, and can’t move a piece back to the tri it was pushed out of.

The board:

First of all, we need some graphics. I drew a quick SVG Taasen board in Inkscape:

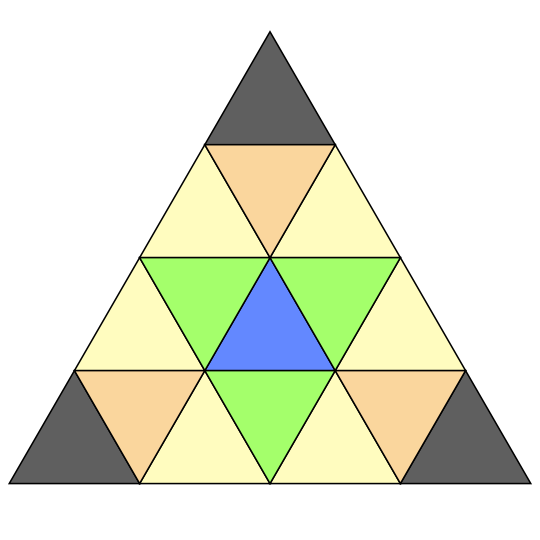
We probably need a numbering system. We have a couple of choices:

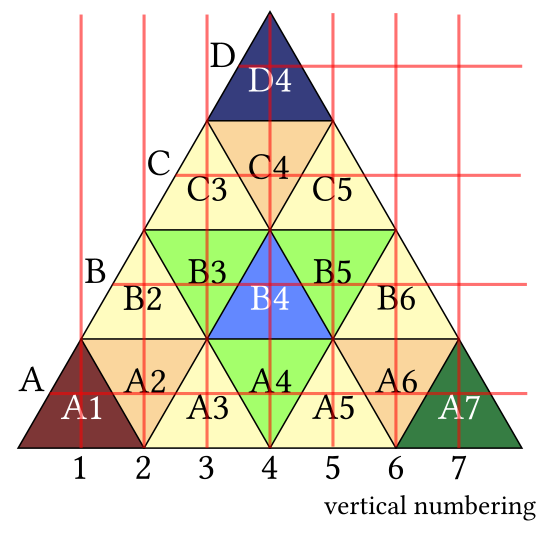
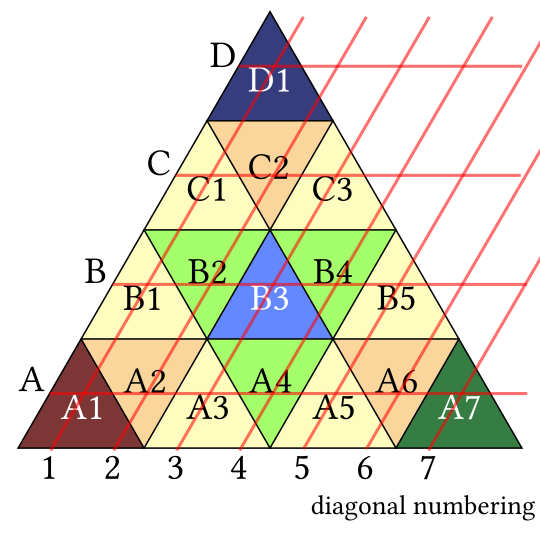
I’m going to go for the vertical number system for the sake of symmetry between red and green.

Counting game states

The game, like many games, can be thought of as a finite state machine. Each arrangement of the pieces on the board is a state the machine can be in, and the moves of the game are transitions between states.

How many states are there? We may be counting some that can’t be reached in actual play, but for now let’s not worry about that.

Well, there are three corner tris (which can each have 0-3 pieces of the same colour) and 13 central tris (which can each have one piece or none). Each piece can also be removed from play.

Assuming all the corner tris are no longer occupied by multiple pieces, we have $$\sum_{n=1}^9 \frac{16!}{(16-n)!}$$possible arrangements of the 1-9 pieces. The result is 4,734,260,416 game states not counting ones with multiple pieces on the starting squares. That’s a big number, though small compared to games like Chess and Go which Taasen is inspired by. However, a lot of these states are already win states. A lot more are probably inaccessible in the game.

Computer representation of game states

What would be a pretty minimal representation of a game state? Well, we could simply list the locations of all nine pieces as a string, as well as the player to move. For example, sorting it RGB, and TSP within each colour, the starting configuration is “A1A1A1A7A7A7D4D4D4″. If a piece has been removed, we could write say, X instead of its coordinates.

A more compact representation might be to use an integer. Why is it so important to represent the data minimally? Well, if we’re going to be trying to generate the entire game tree (something I’m considering), and there are billions of states, that’s going to be gigabytes of data!

With 16 tris on the board, each one can be given a number from 0 to 15, which is 4 bits of data. We can represent removed pieces with the invalid central tri B4.

So here’s another numbering scheme for 4 bits per piece:

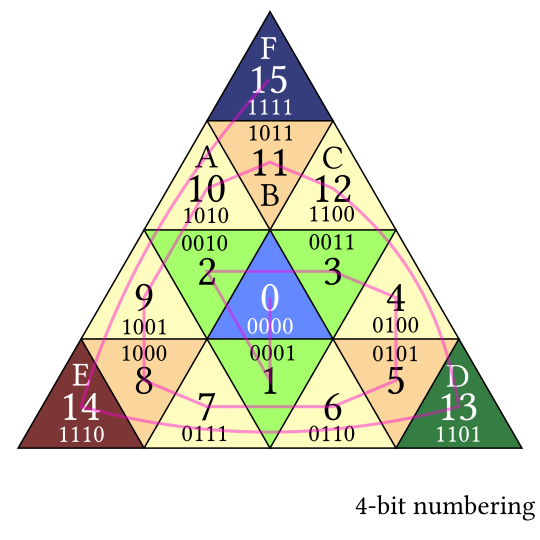
The position of nine pieces is then represented by a 36 bit number. That’s less than ideal actually: a standard integer on a 32-bit computer is (shockingly!) 32 bits, or four bytes. Is there a way we can shave off four bits? Previously we counted 4,734,260,416 game states, and that was an underestimate. A 32-bit integer can represent 4,294,967,296 different states, so that’s not enough.

But actually there may be a solution in C or C++: bit fields. This can apparently (depending on the implementation) let us pack the data into some arbitrary whole number of bytes and give a convenient way to read the fields. So we could get away with using five bytes even though that’s not the size of an integer.

Using five bytes gives us an extra four bits to play with. This might be used because there is some important information we need to know about a given game state not given by the list of pieces:

• whose turn it is
• if a piece was pushed on the previous turn, which piece it is and the tri it’s not allowed to return to
• if a blue piece was moved, which piece it is

Since a blue piece may be used to push another piece, both of these may be relevant. So we’ll probably need an extra byte. RGP TSP

Here’s our game state then:

• 4 bits: location of Red Thaum
• 4 bits: location of Red Sciane
• 4 bits: location of Red Paupil
• 4 bits: location of Green Thaum
• 4 bits: location of Green Sciane
• 4 bits: location of Green Paupil
• 4 bits: location of Blue Thaum
• 4 bits: location of Blue Sciane
• 4 bits: location of Blue Paupil
• 1 bit: 0 for Red to move, 1 for Green to move
• 2 bits: 00 no Blue piece moved, 01 Blue Thaum moved, 10 Blue Sciane moved, 11 Blue Paupil moved
• 3 bits: 000 no piece pushed, 001 own Thaum pushed, 010 own Sciane pushed, 011 own Paupil pushed, 101 blue Thaum pushed, 110 blue Sciane pushed, 111 blue Paupil pushed [so the first bit is 0 if no blue piece is pushed]
• 4 bits: location pushed piece is not allowed to return to
• 2 bits: we don’t really have a use for these so let’s just encode the victory state: 00 game not ended, 01 Red victory, 10 Green victory, 11 Draw

and that adds up to 36+12=48 bits or six bytes.

Example game

Here’s an example of how this representation would function in practice:

• the starting state of the game as a hexadecimal string is EEEDDDFFF000.
• Suppose Red begins by moving her Thaum from E to 8. Then the first part of the string becomes 8EEDDDFFF. For the last three nybbles:
• • The first bit is 1 (Green to move); no Blue piece was moved so the next two bits are 00; no Blue piece was pushed so the next bit is also 0; the first nybble is thus 1000 or 8.
  • No piece was pushed, so the first two bits of the next nybble are 00. This means there is no location it’s not allowed to return to, so that will be set to the null value 0000. Thus the second nybble is 0000 or 0.
  • The first two bits of the final nybble are 00 as mentioned. Both players still have pieces and valid moves, so the game has not ended and the second two bits are also 00. Thus the final nybble is 0000 or 0.
  • The game state after Red’s move is now 8EEDDDFFF800.
• Now suppose Green moves the Blue Paupil down from F to B. The first part of the string becomes 8EEDDDFFB. For the last three nybbles:
• • The first bit is 0 (Red to move); the Blue Paupil was moved so the next two bits are 11; no Blue piece was pushed so the next bit is 0. So the first nybble is 0110 or 6.
  • No piece was pushed so the second nybble is 0000 or 0.
  • No piece was pushed and the game is not over so the third nybble is 0000 or 0.
  • The game state after Green’s move is now 8EEDDDFFB600.
• Since Green moved the Blue Paupil in the last turn, Red can’t move it; all other pieces except her Thaum are blocked in, so she can only move that. Suppose she moves it from 8 to 9 to engage the Blue Paupil. The state becomes 9EEDDDFFB800.
• Green moves her Sciane from D to 5. 9EED5DFFB000.
• Red moves her Thaum from 9 to 2. 2EED5DFFB000.
• Green moves the Blue Paupil from B to A. This is adjacent to the Red Thaum on 2, and therefore triggers a push. Red has the choice of moving to 9, or crossing the sea to escape. She chooses to move across the sea to 1. The state begins 1EED5DFFA, and for the remaining nybbles:
• • The first nybble is 0110 or 6.
  • A Thaum was pushed so the next two bits are 01. The tri it cannot return to this turn is 0110 so the next two bits are 01. So the second nybble is 0101 or 5.
  • The first two bits of the next nybble are 10. This is not a victory state so the final two bits are 00. So the final nybble is 1000 or 8.
  • The game state after Green’s move is now 1EED5DFFA658.

That should illustrate all the main principles.

Exporing the game tree

So we have a representation of a gamestate. Now what we need is a rule for going from one valid game state to others.

Let’s first of all list the possible moves from each tri:

• 0: none (dead piece)
• 1: 2,3,6,7
• 2: 1,3,9,10
• 3: 1,2,4,12
• 4: 3,5
• 5: 4,6,13
• 6: 1,5
• 7: 1,8
• 8: 7,9,14
• 9: 2,8
• 10: 2,11
• 11: 10,12,15
• 12: 3,11
• 13: 5
• 14: 8
• 15: 11

The pieces threatened with pushing after a move to a particular tri are almost the same, but 1,2, and 3 do not threaten each other so the list is slightly different.

So now we might want to explore the game tree.

First of all let’s imagine writing out the entire game tree to figure out how much disc space we’d need if we tried. For each state, we’d have the state itself (as an index) and a list of possible next states. The index and potential next states each fill five bytes.

As an overestimate of the number of possible moves, there are potentially six movable pieces, each of which might be able to move to one of four tris, each of which might provoke up to three possible pushes. So that could be as many as 72 possible moves - in practice it would be significantly smaller because most tris do not have that many moves or pushes available to them. That means each node (game state) could take up to 360 bytes, and if there really are billions of possible states, that could mean many hundreds of gigabytes to an entire terabyte. I might have enough space left on my hard drive but it would be doubtful! And searching through that mess would be a nightmare.

But maybe it’s not that bad. And we could always generate the first few (hundred?) plies on the tree and then stop and see how many are already winning states?

Working out the possible next moves

To generate the whole tree or part of it, we need an algorithm to work out the next possible game states from a given game state.

It would go something like this:

• check whose turn it is to move
• for each of that player’s pieces and the blue pieces
• • check if it’s a blue piece that has just been moved; if so, abort
  • look up the tris it can potentially move to
  • check if the piece has just been pushed and if it has, remove the tri it was pushed from from the list of potential moves
  • check each potential move against the other pieces to see if that tri is already occupied; if so remove that from the list of potential moves
  • check if each potential move would cause a push
  • • if so:
    • • for each piece that could be pushed, check its potential destinations
      • remove the destination that the attacking piece is entering
      • check each destination against the other pieces and remove if occupied
      • for the remaining pushes, generate the next game state for each one
      • if there are no remaining pushes, generate a state where the pushed piece has been removed
    • if not:
    • • generate a game state with that potential move
• output the list of potential moves

I’m going to prototype this in Python just to make sure the algorithm makes sense. While the bitfield representation will be necessary for any sort of large scale tree generation, for testing the algorithm, I’ll just use a string representation: hexadecimal for the locations, R or G for whose turn it is to move, -/T/S/P for a blue piece moved, -/R/G/B for the colour of a pushed piece, -/T/S/P for the piece that was pushed, hexadecimal for where it was pushed from, and -/R/G/D for win state. I’ll use a nice, easy-to-understand Class.

Since this post has already gotten quite long, I’ll cut it off here and start coding. Results will hopefully follow soon!