Time Travel

originally posted at https://canmom.tumblr.com/post/143474...

In a previous post, I answered a question with a fairly narrow scope: if you brought back a modern phone or laptop, what use would it be in The Past? Could you reproduce it?

But ultimately questions of ‘bringing stuff back’ depend rather a lot on the model of time travel you adopt. So this is a post about time travel models, paradoxes, possible connections between time travel fantasies and actual physics (albeit rather flimsy ones), etc.

Contents:

So what’s it like to travel back in time from the traveler’s perspective?

Time travel stories tend to portray it in a couple of ways.

Time travel stories also differ on things like whether the time machine travels with you, how to resolve the complications of relative motion between entrance and exit, how much you can take with you, etc. (The relative motion question is an interesting one, which we’ll definitely consider in detail later in the post.)

One question that I see addressed less often is what happens to matter that’s already present in the region you manifest after time travelling. Unless you’re travelling in space, there’s usually air there. This tends to be addressed only if you end up time travelling into a rock - usually it’s shown that you simply replace whatever was there. Sometimes you might have a 'swap’ happen - whatever was at the destination point is moved to the place and time where you entered the time machine, and you replace the corresponding region at its original place and time.

All of these choices are of course driven by the plot and aesthetic needs of the story - whether time travel is supposed to be something fun and adventurous, or developed by massive sinister agencies, etc. etc. But they are also quite important for determining what the time traveler can and should pack with them. Beyond listing possibilities there’s not much more I can say about them.

The stickier question: how do you deal with causality?

Dealing with the paradoxes and headaches of being able to affect your own past is one of the main subjects of time travel stories. And there is no straightforward answer: ultimately, when time travel enters the picture, some of our intuitions about cause and effect have to go.

If you’re particularly concerned about logical consistency, you roughly have two choices that I can see…

For some media that do these two kinds of time travel:

Both these models basically present the idea that each character’s past is 'fixed’: the time travel actions don’t rewrite them with another character whose history is different. Because if that’s possible, you start hitting sticky questions like: “when” does the rewriting take place for the time traveller? What happens if the “rewritten” time traveller no longer wants to time travel, or take the actions that precipitated the rewriting?

These two models avoid the infamous Grandfather Paradox as follows: in the first, you will never successfully travel back in time to prevent your own conception. Any attempts to travel back in time and prevent your own conception are already part of history, and they failed. In the second, you can prevent the conception of a different version of yourself in another timeline, but that has no effect on you.

Time travel media deals with some or all of these questions, depending on its intentions.

Many stories, such as Back to the Future, use a view of time travel that’s designed with the progression through the story in mind. While events in the films may be happening at different times, two plotlines develop in parallel, and when something happens in the 'past’, it affects the 'future’ only at the corresponding point in the film.

Homestuck in some ways makes this explicit, with the handwavey concept of 'circumstantial simultaneity’ linking events in entirely separate timelines. More broadly Homestuck has a rather involved model of time travel that combines the above two models.

What does physics have to say?

Causality and physics is something that philosophers like to grapple with (as part of their general grappling with the concept of causality). It turns out the causality is actually a surprisingly sticky notion in most physical theories.

We’re particularly concerned with time travel, here, rather than the possibility of the future being undetermined by the present. So while Newtonian physics has its problems of it being possible for certain things to suddenly happen with no way to tell from the present, we won’t talk about that.

After we’ve considered an instance where time travel is possible in special relativity, and a discussion of closed timelike curves in general relativity, I will talk about the question of relative motion in portrayals of 'sudden’ time travel.

The tachyonic antitelephone

Instead let’s start with the “tachyonic antitelephone” in special relativity. (I love that name.) For this little section on SR, it’s potentially helpful to check the first parts of my primer on special relativity. (Feel free to ignore the bits on covariant notation and four-vectors). But if you don’t want to read that, I’ll try and repeat all the relevant stuff here!

So, in special relativity, we think of everything following a 'path through spacetime’. That is, rather than everything 'moving around through space’ as 'time’ advances, we consider each thing to have a position in both space and time, and moving between different positions in global space and time as their own personal experience of time - their 'proper time’ - advances.

At each point along the path, something following the path has a velocity (in a particular reference frame) determined by the direction of the path in spacetime. Depending on its velocity, the path at this point can be placed into one of three categories: timelike if it’s slower than the speed of light, lightlike if it’s exactly at the speed of light, and spacelike if it’s faster than the speed of light.

The important thing is that these categories are the same in every reference frame. That is to say, for any observer travelling at any speed (below that of light), a spacelike path will still be spacelike, a lightlike path will still be lightlike, a timelike path will still be timelike.

Timelike paths will additionally always have a clear direction in time. That is, if you pick two points on a timelike path, and one happens later in global time than the other, that will still be true in any reference frame.

Spacelike paths do not have this clear direction in time. Depending how fast the observer is going relative to the points on the spacelike path, they may perceive one point to be earlier in time, or the other.

The rule in special relativity is that information can only travel on timelike and lightlike paths. This creates a 'light cone’ containing the points in spacetime you are capable of affecting. Nothing I do will change the state of things on the other side of the world at the exact instant that I’m typing; the soonest my actions now could affect the state of things over there is the time it takes a beam of light to travel there directly.

This issue is a bit of a problem if you’re trying to write a story with space travel, because the speed of light is frustratingly slow compared to the distances between stars.

So, what if a message could travel faster than the speed of light? What’s this got to do with time travel?

Basically, you can exploit this property to create a construction called the 'tachyonic antitelephone’. A 'tachyon’ is a general term for 'a particle that travels faster than the speed of light’. It’s called an 'antitelephone’ because, uh, it sounds cool I guess?

What you can do with it is basically send information back to an earlier point on your own timeline. You need a large amount of space to do it on any significant scale, though.

So let’s start with the ingredients. To make a tachyonic antitelephone, you need:

To make sense of a tachyonic antitelephone, let’s start with saying what the ansible does more precisely. Basically we have to answer the question of 'how fast are the ansible’s messages’, but it’s a tricky question because a speed is defined in a particular reference frame. Only something travelling at the speed of light travels at the same speed in every reference frame.

What we will say is this: in the reference frame of the transmitter, the speed of an ansible message is \(ac\), where \(a>1\) and \(c\) is the speed of light. That is to say, the ansible transmits at a fixed speed in its own reference frame; naturally in other reference frames this speed will be different.

So here’s what we do. We begin by getting the relativistic spaceship up to speed. We will say there are two people (or, political bodies) involved: a coalition of planets called the Ekumen, and their envoy Genly Ai. Genly is travelling away from the Ekumen at some relativistic speed - in the diagrams below, about 60% of the speed of light.

(These characters are from Ursula Le Guin’s book The Left Hand of Darkness, one of the best known books in her Hainish Cycle series that created and popularised the word 'ansible’ for an FTL communicator. In the book, Genly is able to use his ansible to maintain real-time conversations with the Ekumen, but in relativity, events are only simultaneous in a particular reference frame. The model of an “ansible” used here is the same as I’ve seen in other expositions of the “tachyonic antitelephone”).

So, at some point, the Ekumen sends a message to Genly via the ansible. They have some query they need a reply to.

Here’s a spacetime diagram the situation looks like in the Ekumen’s rest frame:

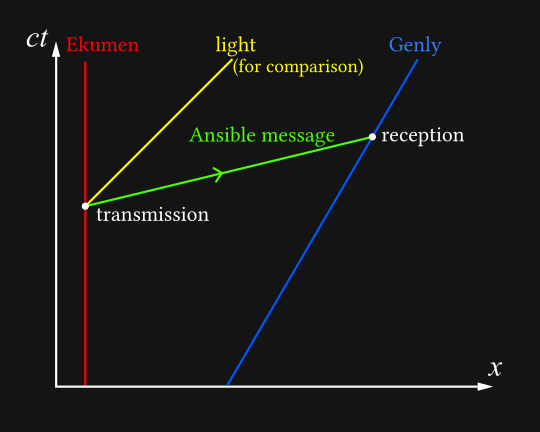
A spacetime diagram, with ct on the vertical axis and x on the horizontal. A red vertical line is marked Ekumen, and a diagonal blue line (steeper than 45 degrees) is marked Genly. A 45 degree line represents light for comparison. A green line marked 'ansible message', less steep than light, connects a point on the Ekumen's worldline marked 'transmission' to a point on Genly's wordlline marked 'reception'.

To find out what this looks like in Genly’s rest frame, we must perform a Lorentz transformation, which moves all the events around - but the slope of the speed of light remains fixed. Inkscape allows you to perform arbitrary matrix transformations, so all of these Lorentz transformations are exact. (Mathematical details can be found on Wikipedia here.)

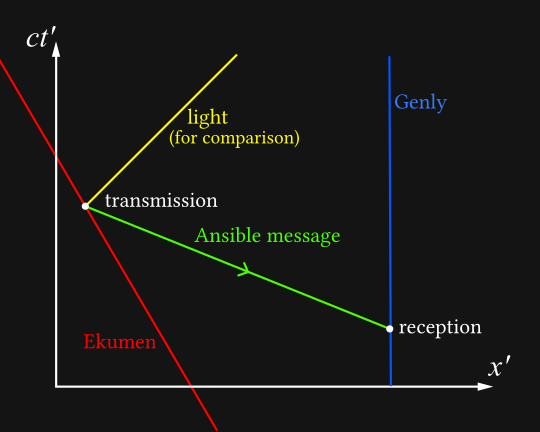
The same spacetime diagram is viewed in Genly's rest frame. In this frame, the Ekumen's worldline points towards the top left, and the point of transmission is now later than the point of reception, so the ansible message points towards the bottom right.

We recognise this as Genly’s rest frame because his spacetime path forms a straight vertical line. We can already see the beginnings of a paradox here: in Genly’s frame, the message arrives long before it’s sent. This is unintuitive, but we have’t yet introduced a true contradiction.

Now suppose that as soon as he gets the message, Genly sends a message back to the Ekumen using his own ansible. The speed of the message is determined in Genly’s frame.

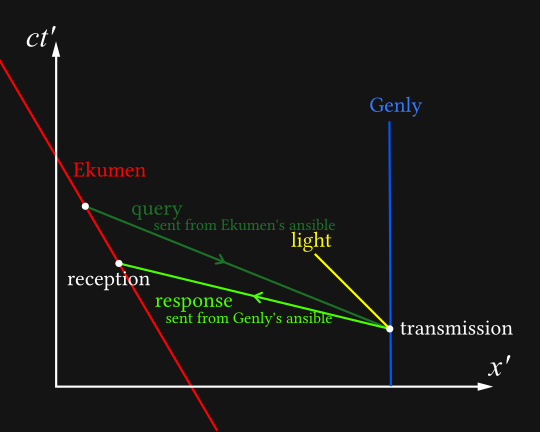
A spacetime diagram in Genly's frame. The transmission has now been relabelled to 'query sent from Ekumen's ansible', and there is a new line representing Genly's response. Genly's response has the same slope as the query did in the Ekumen's rest frame, but it is not as steep as the query's slope in this frame. It returns to the Ekumen's worldline before they sent their message.

We can see the problem now: Genly’s reply arrives on the Ekumen’s timeline before the Ekumens sends its query. Let’s also see it in the Ekumen’s frame:

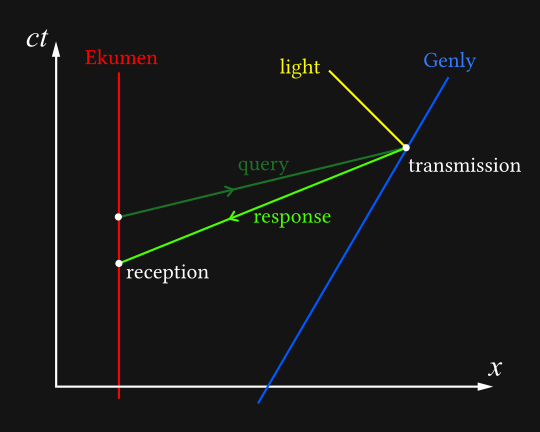
A spacetime diagram in the Ekumen's frame. Genly's response's worldline points towards the bottom left, and arrives before the Ekumen's query is transmitted.

As far as the Ekumen is concerned, Genly’s message goes back in time even faster than their message was going forwards in time. Of course, they have no inkling of this until the message arrives, suddenly, out of nowhere, with a reply to a question they haven’t yet considered to ask.

Even in this very simple scenario, a paradox could arise. Perhaps the Ekumen, having their impromptu answer, would not think to send the query - and now the query no longer exists, so Genly will not reply. Uh-oh.

Anyway, that’s the tachyonic antitelephone. If you want to send a message into your past, you set up one or more signal relays travelling away from you, whose job is simply to receive a message on your ansible and send it back to you. (Assuming a single consistent timeline, you’ve already received your message.)

The main potential problem of this scheme as a means for setting up time travel stories is that the amount you can send a message back in time is limited by the speed of your message, the speed of the relay (which must be travelling at relativistic speeds to be useful), and how far away the relays are. Getting a message back in time requires a lot of space to play with. And if you want to send yourself, personally, back in time, you need to be on board an FTL spaceship for an extended period making the round trip.

How much time would our intrepid time traveller experience while travelling along a spacelike curve? It’s a bit of a weird question.

Let’s consider the other two cases first. For timelike curves, the proper time elapsed along a curve is given by applying the metric and integrating - the rule for a straight constant-speed line is \(c^2 \Delta\tau^2 = c^2\Delta t^2 - \Delta x^2\) where \(\Delta\tau\) is the elapsed proper time, \(\Delta x\) is the distance moved in space in some inertial reference frame, and \(\Delta t\) is the time elapsed in the same frame. If you try to apply this to lightlike lines, you find that the metric is 0 for any length of line (by definition), so you can’t use proper time to parameterise a light line (you resort to using any affine parameterisation).

So what if you try to use that rule for spacelike worldlines, i.e. faster than light travel? To be spacelike, the line has to have \(\Delta x>c\Delta t\), with the consequence that the square of the proper time elapsed is now negative - the proper time elapsed is now an imaginary number.

What does this mean? Um. Wow. I have no idea. It means we’re probably asking a bad question. But if we take the naive interpretation, and assume going forwards in imaginary time is indistinguishable from going forwards in real time, we find that you have a sort of inverse time dilation effect - the slower you go, i.e. the closer to the speed of light, the more time dilation you experience.

But how slow you go also affects how far back you can travel in your personal timeline.

It’s at this point that the original draft of this post went into a more detailed mathematical analysis that was a couple of times longer than everything I’ve written so far. I’m therefore splitting it here; stand by for another post on the mathematical details of the antitelephone.

A questionable interpretation of antimatter

So that’s what plain old classical special relativity has to say: FTL == time travel. What about when things get quantum?

To be honest, explaining this would require its own post introducing the basic ideas of quantum field theory, Feynman diagrams etc. So we’ll leave this for the future. Unless, of course, I time travel from the future to inform me of what I’m going to write in this section.

If you want a sneak preview, take some time to read up on antiparticles. Basically I believe you can connect certain time travel story tropes to the Feynman diagrams you use in quantum field theory calculations, based on the fact that antiparticles can be understood as the corresponding particle travelling backwards in time. It’s kind of spurious, but it might be a fun angle to explore quantum field theory from.

General relativity and closed timelike curves

Of course, special relativity is not our full theory of spacetime, and cannot describe gravity. For our current best large-scale picture of the universe, we have general relativity, in which spacetime is distorted in many ways by mass.

An object in special or general relativity follows a curve through spacetime. You have some parameter, like proper time, and for each value of proper time, you get a location and time (in a particular reference frame).

The general rule is that massive objects follow a path that is 'timelike’, which means at any individual point, it’s slower than the local speed of light. The jargon 'closed timelike curve’ therefore means a route through spacetime which is everywhere timelike - it can be followed by a massive object - but returns to the same spacetime position - same position and time - that it started.

Are there such things? Absolutely. They normally crop up when you have something rotating. I started by following the discussion in this 1993 Caltech lecture by Kip Thorne, who seems to be the guy who was doing all the time travel research in the early 90s, but I’ve found another more recent paper that is maybe a bit more accessible.

Back in 1937, a guy called Willem Jacob Van Stockum was the first to come up with a spacetime to support CTCs. His spacetime involves nothing but an infinitely long cylinder of rotating homogeneous 'dust’; the result is that a closed timelike curve can be found travelling around the cylinder in the correct direction. By flying near this timelike loop and performing a suitable number of orbits, you can go back in time and return to any position in spacetime. Back in 1993, it was unknown whether the same could be achieved with a finite cylinder. I don’t know if that’s been answered since.

A similar situation can be found in a stationary, homogeneous universe entirely filled rotating dust - the “Gödel solution”. (This is the same Kurt Gödel who came up with the Incompleteness Theorems.) The complexities of this are a bit beyond me right now, but I’m hoping to be able to make a future post. But there are closed timelike curves through every point in the Gödel spacetime.

Infinitely long rotating cylinders and fictional universes full of rotating dust are all well and good, but practically speaking, don’t lead to any realisable form of time travel. So let’s move on to spacetimes that are ever-so-slightly more realistic.

This is where Kip Thorne’s lecture starts to use much more complex maths, talking about a concept called a Cauchy Horizon that I don’t fully understand. For the sake of finishing this post, we’ll go over the other possibilities in summary.

The most physically realistic thing to consider is a rotating black hole. The geometry of space around a spinning, uncharged black hole with nothing else around it is given by something called the Kerr metric. Most black holes probably fit this metric. There are closed timelike curves in the Kerr metric, but I’m not able to follow whether you have to pass beyond the event horizon to follow them.

The other major one to consider is the case of ’wormholes’, also known as Einstein-Rosen bridges (though this may refer to a specific sort of wormhole). Kip Thorne uses this in the introduction of one of his papers as an example of a spacetime with CTCs.

Wormholes are a 'topological’ feature of spacetime, which you find in a number of metrics. Basically it means there are two points in spacetime connected in two different ways, one of them being a relatively short tunnel that bypasses the intervening space and time.

So for example, the ends of a wormhole might be located here on Earth right now, and at the edge of the Solar System in a year’s time. A particle would then be able to pass through one mouth of the wormhole and emerge at the other end without experiencing a year worth of time.

It turns out that the Schwarzchild solution - one of the first solutions to general relativity discovered, which describes spherically symmetrical non-spinning distributions of matter such as a non-spinning black hole - contains a wormhole to another 'universe’, which has a 'white hole’ matching the Schwarzchild black hole. (I haven’t the foggiest idea how you show that comes out of the Schwarzchild solution!) However, the wormhole would apparently close before any matter could reach the other side, and various other conditions prevent the wormhole forming outside of the idealised Schwarzchild case. Sorry for being vague on the details, I’m rather out of my depth here.

It’s a nice idea in principle. However, it can be demonstrated (apparently) that in standard general relativity, you always need 'exotic matter’ for a traversible wormhole. The field equations of general relativity tell you what mass distribution you need for a given spacetime metric. With familiar, everyday metrics, all the mass is positive, but for some of the wackier metrics like wormholes, you need matter with negative mass in some parts of spacetime - something which does not seem to exist.

If exotic matter is allowed, you can construct a Morris-Thorne wormhole, which was described by Kip Thorne and his student Mike Morris in 1988 and requires a spherical shell of exotic matter around the wormhole. That would mean anything trying to go through the wormhole would have to go through the exotic matter shell. Apparently it is also possible (says Wikipedia) to find wormhole solutions where there’s a route through the wormhole which doesn’t go through the exotic matter.

Further issues start to crop up when you bring quantum mechanics into the picture. This is speculative, of course: we do not yet have a conclusively demonstrated theory of quantum gravity (though physicists and mathematicians have made a number of tries!), so any sort of quantum + wormhole is probably using a bit of a fudge. (A very clever fudge, no doubt, that goes over my head. And now you’ve just splattered tasty fudge all over the wall. Stop throwing the fudge around, physicists!). So the results are unclear. There’s speculation that a Weird Quantum Thing could force wormholes to close without there being closed timelike curves. There’s apparently also proof that closed timelike curves don’t necessarily break quantum mechanics. There’s also speculation that Weird Quantum Shit could provide the 'exotic matter’ and keep a wormhole open.

What to conclude? General relativity isn’t, inherently, nearly so worried about causality as we are. But for some reason, all the causality violations we’ve considered have some limitation so we have no straightforward lead on achieving time travel in our universe. Weird Quantum Shit may be involved, but if so, it’s not clear what the consequence will be.

The sticky question of relative motion

Time to come a long way down from the kind of relativity stuff that goes over my head, and back to good old Newton.

Occasionally, science fiction writers notice that the Earth is travelling around the sun, the sun around the centre of the galaxy, etc. etc. and connect it with their time travel plot.

So you have a time traveller. She turns on her time machine, and goes back in time a day, in a portrayal where time travel is immediate - disappear from one place and time and appear somewhen and somewhere else.

In most time travel stories, she turns up on Earth, in the same place on the surface of the Earth that she left.

Some time travel stories instead say that, because the Earth was in a different place a day ago, if you time travel “in the same place” you will find yourself floating in space because the Earth hasn’t reached that point when you arrive.

I remember getting a big book of 2000AD’s Strontium Dog comics some years ago. I never read much of it, but they made heavy use of this plot device in the first few chapters - the protagonist makes use of it to escape from sticky situations into space.

So in principle, this isn’t necessarily a bad plot device. The problem comes when you try to work out exactly how fast everything is going.

One of the most fundamental principles of Newtonian and special relativistic physics is that there is no 'preferred’ frame of reference. That is, suppose we have a reference frame - a perspective that amounts to a coordinate system for every point in space and time - where the rules of physics follow Newton’s laws in their simplest form, e.g. the kinetic energy is \(\frac{1}{2}mv^2\), particles travel in straight lines unless acted on by an external force, etc. etc.

Suppose then that we consider everything from another perspective, where the origin of the coordinate system is travelling at a constant velocity relative to the original coordinate system. In other words, from the perspective of someone travelling past the first observer at a constant speed and direction.

We find that, regardless of the speed of this other frame, we can transform the motion of particles into the new frame and Newton’s laws still have the same, simple form.

You can read about these ideas in more detail in this post I did on mechanics some time ago.

This symmetry of spacetime is very important, and leads to such things as conservation of energy and momentum by Noether’s theorem, which I will properly get into one day! But they also have a very direct implication: any velocity we define for an object is relative to a particular frame of reference, and vitally, there is no “correct” frame of reference, but a class of frames of reference called “inertial” frames where physics is in its simplest form.

As an example: if you’re moving past me at \(2\thinspace\mathrm{ms^{-1}}\), we can identify two obvious reference frames. In my rest frame, you might have a velocity of \(+2\thinspace\mathrm{ms^{-1}}\) in the \(x\) direction, and correspondingly in your rest frame I would have a velocity of \(-2\thinspace\mathrm{ms^{-1}}\) in the \(x\) direction. Neither of these frames is the 'true’ frame, and neither of us fundamentally has a velocity of \(2\thinspace\mathrm{ms^{-1}}\) in any direction. We could just as well use a frame in which I have a velocity of \(46\thinspace\mathrm{ms^{-1}}\) and you have a velocity of \(48\thinspace\mathrm{ms^{-1}}\); in all cases we could still calculate whatever it was we wanted to calculate.

So when you say the Earth is travelling at a particular speed, the immediate question is “in what reference frame?”.

In everyday life, we use the reference frame of the surface of the Earth at a particular point - which is not an inertial frame, as the Earth rotating and being accelerated by the sun and the galaxy etc., but in many circumstances can be approximated as one - as a sort of implicit frame of reference when we talk about, say, the speed of a car. So when the driver of a car says they’re travelling at 40 miles per hour, that is 40 miles per hour relative to the road underneath.

There is a good reason for this, of course: friction between moving objects and the ground means all objects will eventually slow to a stop on the ground. So treating the ground as being 'at rest’ is extremely natural.

Aircraft pilots need to take a more complex view, distinguishing (for example) between the airspeed of an aircraft - the speed relative to the air immediately around it, which may be moving because of wind relative to the ground - and the speed of the ground. The airspeed is what is important to the mechanics of flight, while the ground speed is of course important for navigation. Spacecraft operators have to take a more complex view still, often working in (for example) a non-rotating frame centered on the Earth when plotting out orbits.

So if a time machine is supposed to make you travel in time “in the same place”, where you appear after your time travel is dependent on what reference frame you use.

Let’s go over a few possibilities that seem 'natural’, staying for now in Newtonian physics:

If we inherit the velocity from the time machine:

If we try to find a 'preferred frame’ despite all of the above: The main factor is the speed of the milky way galaxy itself relative to… something. There’s two possibilities for working out the velocity of the Milky Way.

On top of that motion, we add the sun’s motion relative to the centre of the Milky Way (about \(220\pm6\thinspace\mathrm{kms^{-1}}\)), with the direction such that the Sun’s motion relative to the CMBR is about \(370\thinspace\mathrm{kms^{-1}}\). Then we have the Earth’s motion around the sun, which is a comparatively small \(30\thinspace\mathrm{kms^{-1}}\) in a direction that varies over the course of a year.

Should we treat one of those frames (the CMBR frame, or the co-moving Hubble flow frame) as the 'correct’ frame for our time machine’s rest frame? Well… the fact that we have two options that differ by about \(80\thinspace\mathrm{kms^{-1}}\) already makes this questionable! These frames may be associated with the formation of the universe, but in terms of physics there’s nothing particularly special about them.

In any case, if you used this assumption, the radius of the Earth is about \(6300\thinspace\mathrm{km}\), so time travelling for a few seconds would leave you either deep underground or thousands of kilometers off the ground unless you’re absurdly clever. And any further time travel than that? The radius of the Earth’s orbit is about \(1.5\times10^8\thinspace\mathrm{km}\), which means time travelling for more than four days could take you as far as the sun if you got the direction right.

To me, the difficulties of picking a suitable reference frame for time travel are such that it makes most sense to have a 'time anchor’ that stays sitting on the surface of the Earth, and your time machine can use as a reference point for your destination. This fits more with the idea of a 'time portal’ than a time machine that can be used anywhere for arbitrary amounts of time. Of course, you can also get away with ignoring it, or coming up with some handwavy explanation of how the time travel frame is fixed to the Earth.

A cool thing to do with time travel

So like, to my shame, I’m going to report something I first heard about in the infamous LessWrong megafic “Harry Potter and the Methods of Rationality”. But this is a genuinely cool idea and worth salvaging from that mess.

Having a look around, it seems rather like this idea was first presented in 1991 (the year I was born!) by a 'roboticist and futurist’ (lol) called Hans Moravec in this article. This article is great fun to read. It begins with a survey of supposed possibilities of time travel in physics, before moving on to various simple logical circuits that exploit self-consistent timelines with time travel to solve problems that would take a very long time on an ordinary computer.

Please be warned to take all this talk about time travel possibilities within physics with a huge grain of salt. This is sort of 'fun thought experiment’ territory rather than 'concrete prediction of solid physics’.

Essentially, you can use causality violations and time travel to create a situation where the only consistent timeline is one where you magically get the answer to a calculation. Thus you turn your computer on, time itself does the calculation for you, and you get your answer in no time at all.

This can be used to, for example, factorise a large number, which means your time travelling computer could be used to break the main form of encryption we use today even better than a quantum computer.

Iterative algorithms, which take the result of a calculation and improve upon it, stopping when they reach a 'fixed point’ where each iteration step does not change the result, can be fitted to a time machine to leap instantly to the fixed point. Similarly, Moravec sketches how a time travelling computer can be used to instantly solve NP-complete problems.

I won’t repeat everything in this paper. But it’s a neat idea.

Do we have a conclusion?

Time travel is pretty cool. That’s my conclusion.

Comments

Add a comment
[?]