How big could you build an enormous concrete cube?

originally posted at https://canmom.tumblr.com/post/864325...

I was asked anonymously on Tumblr...

I like the name on the moon article, we have had similar flights of imaginative nonsense and did the math for it. However, one of my favorites is simply the creation of a solid (concrete) cube, the super power is the country that can build it or then seize it (hypothetically). It is too big to construct, too costly to build, too ridiculous... but that is why we like it. Do you fancy having a go at the idea?

Hi anon. A few things occur to me that would be relevant here: the rate at which you could make the concrete, and the structural integrity of the Cube. (A giant Cube must be a proper noun. It is only fitting.)

This is not going to be as thorough as the moon thing, since I know much less about buildings than I do about space.

Worldwide cement production is currently about \(4\times 10^9 \unit{kg}\) a year according to the US Geological Survey 2013 report. Of course, that’s produced all over the world on various scales, and transporting it to the Cube would be very difficult. I suspect you’d want to build your Cube next to some enormous limestone deposits (which ones depend on your country), and build loads of quarries and cement plants. (Here’s an illustration of the process, though perhaps you can skip storage and go straight to the Cube). Per Wikipedia, you can get more concrete by also using pozzolan.

This is reported in a variety of places to produce about 5% of humanity's CO₂ emissions, about half from the reactions to make the cement and about half from heating up the kilns. But then, you’re building the Cube. Perhaps you’re not worried about climate change.

You’d need to mix that cement with water and an aggregate, which means you need vast quantities of water and gravel as well as your vast quantities of cement. Of course, you also need to generate enough power to heat your kilns, which takes fuel. To make strong cement, you need things like plasticisers. You probably also want to reinforce your cube with steel in the directions where tensile strength is important.

How big can the cube be? Let’s imagine you use all the tricks in the concrete-maker’s book, and make the strongest concrete you can for the bottom layer of the cube. Apparently, this amounts to a compressive strength of ~130MPa. An old newspaper article says this was achieved using a glacial aggregate of small particles. A team from the University of Tehran has apparently (CW for weapons, Americans planning to bomb people) gone even higher, achieving as much as 350Mpa compressive strength using steel fibre and quartz aggregate.

This can tell us the maximum height of the cube. I’m not sure the density of these super-high-strength concretes. Wolfram Alpha gives a median concrete density of \(1.1\unit{g\,cm^{-3}}\) and an upper bound of \(2.4\unit{g\,cm^{-3}}\). On the assumption that we vary the kind of concrete we use and use less strong, lighter concretes higher up the Cube, I’ll just assume the median.

Each little area of concrete must support the entire height of the stack of concrete above it, on average. The weight per unit area \(P\) of a stack of concrete of height \(h\) and density \(\rho\) under gravitational acceleration \(g\) is just \(P=\rho gh\), so the maximum height we can build to without the bottom layer failing is \(\frac{P}{\rho g}\). This gives us a height (edge-length of the Cube) of \(32 \mathrm{km}\). The total volume of concrete we must fill our cube with is then \(h^3=34\,000\unit{km^3}\). This would mass about \(4 \times 10^{16}\unit{kg}\), so if we dedicated the entire world’s current concrete production to filling the Cube, it would take us about 10 million years.

Here’s a scale picture of that Cube next to the largest buildings in the world. The little red sliver is the Burj Khalifa…

This Cube is around four times the height of Mt. Everest. Here it is in London:

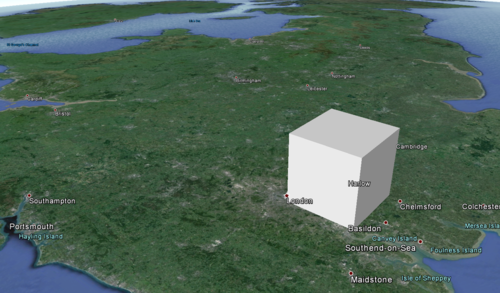
Clearly there’s no point trying to build a cube that large, even if we could drastically up cement production. That’s the timescale of evolution (our last common ancestor with orangutans lived about 14 million years ago, and with gorillas and chimps around 6-8 million years ago) and continental drift (here’s what the world looked like 14 million years ago), and no (presumably Cube-centred) human society could hope to live that long.

If we take more a standard ‘high strength concrete’ than the Iranian super-concrete, we get a cube around 4km to a side, taking a mere 14,000 years to fill. And if we forget pushing the limits of compressive strength and instead build a Cube as tall as the Burj Khalifa, we’re down to about 150 years.

Mind you, I’m assuming here that the world is producing concrete at its maximum capacity, and that the rate-limiting factor is making the concrete. You could probably get a different answer if you base it on the time the concrete takes to set and strengthen.

Another thing that I haven’t considered is that there are plenty of ways for a huge bulk of concrete to fail that don’t involve literally crushing the bottom layer. Cracks would form as the Cube shrinks over time, and they would propagate easily. Earthquakes would be very bad news. Over time, the Cube would be weathered down to a blob, and then a more standard shaped mountain. The remains will create vast amounts of limestone sediment.

Finally, much like other large volcanoes and mountains, the Cube will also sink into the Earth, until it reaches isostatic equilibrium with the mantle. Whatever landmass you’re on could become quite a lot damper in the parts which aren’t under the Cube.